Moon Seung Hyun

[Algorithm] 유클리드 호제법(최대공약수 구하기) 공부


정의

유클리드 호제법(- 互除法, Euclidean Algorithm)은 2개의 자연수 또는 정식(整式)의 최대공약수(Greatest Common Divisor)를 구하는 알고리즘의 하나이다.

호제법이란 말은 두 수가 서로(互) 상대방 수를 나누어(除)서 결국 원하는 수를 얻는 알고리즘을 나타낸다.

2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다.
이 성질에 따라, b를 r로 나눈 나머지 r'를 구하고, 다시 r을 r'로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수이다.

이는 명시적으로 기술된 가장 오래된 알고리즘으로서도 알려져 있으며, 기원전 300년경에 쓰인 유클리드의 《원론》 제7권, 명제 1부터 3까지에 해당한다.

- 위키백과, 우리 모두의 백과사전.



설명

글설명

  1. GCD(270,192) - 270과 192의 최대공약수 찾기
    • A=270, B=192
    • A ≠ 0
    • B ≠ 0

    270 = 192 * 1 +78

  2. GCD(270,192)=GCD(192,78) - 이기 때문에 192와 78의 최대공약수 찾기
    • A=192, B=78
    • A ≠0
    • B ≠0

    192 = 78 * 2 + 36

  3. GCD(192,78)=GCD(78,36) - 이기 때문에 78과 36의 최대공약수 찾기
    • A=78, B=36
    • A ≠0
    • B ≠0

    78 = 36 * 2 + 6

  4. GCD(78,36)=GCD(36,6) - 이기 때문에 36과 6의 최대공약수 찾기
    • A=36, B=6
    • A ≠0
    • B ≠0 36 = 6 * 6 + 0
  5. GCD(36,6)=GCD(6,0) - 이기 때문에 6과 0의 최대공약수 찾기
    • A=6, B=0
    • A ≠0
    • B =0, GCD(6,0)=6

지금까지의 과정 :
GCD(270,192) = GCD(192,78) = GCD(78,36) = GCD(36,6) = GCD(6,0) = 6
GCD(270,192) = 6

그림설명

  • 106와 16의 최대공약수 구하기 - GCD(106,16)

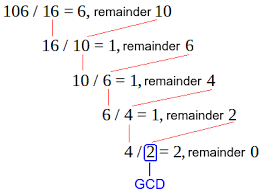
GCD-ex2

관련 코드

파이썬 코드

# 방법1
def gcd(m,n): # gcd == "Greatest Common Divisor"
	if m < n:
		m, n = n, m
	if n == 0:
		return m
    if m % n == 0:
		return n
	else:
		return gcd(n, m%n)


# 방법2
def gcd(m,n):
    while n != 0:
       t = m%n
       (m,n) = (n,t)
    return abs(m)

# 방법3
def gcd(m,n):
    while n! = 0:
	    if m < n:
		    m, n = n, m
	    if n == 0:
		    return m
	    if m % n == 0:
		    return n

자바코드

 public static int gcd(int p, int q)
 {
	if (q == 0) return p;
	return gcd(q, p%q);
 }

자바스크립트코드

Javascript Code to Perform GCD

function gcd(a, b) { // 단, a가 b보다 커야함.
  var R;
  while ((a % b) > 0)  {
    R = a % b;
    a = b;
    b = R;
  }
  return b;
}

Javascript Code to Perform GCD using Recursion

function gcd(a, b) { // 단, a가 b보다 커야함.
  if (b == 0)
    return a;
  else
    return gcd(b, (a % b));
}

function gcd(a,b) {return b ? gcd(b,a%b) : Math.abs(a)}

최소공배수(LCM: Least Common Multiple)

두 수(a,b) 중 어느 한수가 다른 한수의 약수가 아니면
최소공배수 = 최대공배수 * a * b

let LCM = a*b/GCD

두 수(n,m)의 최소공배수(LCM), 최대공약수(GCD) 구하기

function gcd(a,b) {return b ? gcd(b,a%b) : Math.abs(a)}

function solution(n, m) {

  let a = n > m ? n : m
  let b = n < m ? n : m
  let k = gcd(a,b)

  return [k, a*b/k]
})




2023

Flutter 맛보기 1

3 분 소요

직방 기술지원팀 기술공유 세미나 중 플러터를 소개한 내용입니다

Back to Top ↑

2022

Back to Top ↑

2019

[Tutorial] Storybook과 Bit을 활용한 UI 컴포넌트 관리(Workflow)

1 분 소요

회사에서 프론트엔드 개발원칙을 SFC(Single File Component)에서 UI 컴포넌트를 기준으로 CDD(Component Driven Development)를 진행하려고 한다. 그래서 체계적으로 관리하기위해 Storybook과 Bit을 도입해보고자 한다. 각각의 역할은 ...

[Workflow] 프론트엔드 개발조직을 위한 워크플로 설계

2 분 소요

작성 배경 회사의 작업구조를 페이지 중심 개발에서 UI 컴포넌트 중심 개발로 변경하면서 Workflow를 개선할만한 환경을 구성해야했다. 폐쇄망 기반에서 개발자간 UI 명세서 역할을 할 수 있는 Storybook과 그것을 공유할 Verdaccio라는 구축형 NPM Pri...

[ESlint & Prettier] 개발 관습 설정 in Visual Studio

1 분 소요

회사 프로젝트를 작업하기 전 프론트엔드 개발자들 간의 코드 규칙을 Eslint와 Prettier 설정을 맞춰 관리해가는 방향을 정했다. 아직 협업을 할 경우는 없지만 미래에 인수인계 받거나 협업을 진행할 경우 코드관습이 달라 고생할 경우를 대비하기로 했다. 설정은 작업을 진행하며 ...

[CodingTest] 2019-10-26 SQL문제

최대 1 분 소요

공부겸 코딩테스트 사이트에서 토요일 오전 10시에 백엔드 포지션 테스트를 해준다기에 참여해봤다. SQL문제가 나왔는데 더 좋은 답이 있는것 같아 나중에 기록해두고 수정해보기로 한다.

[CodingTest] 피보나치 수열

1 분 소요

문제 : 피보나치 수열 제 1항부터 입력한 자연수(N)까지의 피보나치 수열 항들의 합을 구하여라.

[Syntax] 새로 알게된 파이썬 문법 정리

최대 1 분 소요

chaning comparison 파이썬은 chaning comparison이라는 신기한 문법이 있다. 참고 if a < b and b < c : (...) 라는 구문이 if a < b < c : (...) 으로 연산된다. 직관적인 문법이 인상적. ...

[DataType] Map & Set

최대 1 분 소요

Set vs Array - 관련기사 Set 유일값들의 배열이 필요할때(distinct) 집합의 개념이 필요할때(차집합, 교집합 등등 자체 메서드들이 많음.) index가 필요 없을때 Array에서 중복값을 없앨때 => ...

Back to Top ↑

2018

SGIS-shpToGeojson

1 분 소요

SGIS에서 받은 지도데이터(.shp)를 geojson으로 변경하는 작업 내용

Back to Top ↑